[bibshow file=ref.bib]
Assim como prometido em nosso último relato, traremos aqui uma apresentação mais detalhada do modelo de Liljencrants-Fant (LF) [bibcite key=fant1985four]. Ora, o modelo LF surge a partir da junção do modelo de Liljencrats com o modelo de Fant, acrescidos do uso de uma fase de retorno, com proposto por Ananthapadmabha1 [bibcite key=ananthapadmanabha1984acoustic].
Durante a preparação desse relatório, pudemos perceber que esse modelo possui uma estrutura mais complexa (tanto para o entendimento quanto para a implementação) do que o modelo de Rosenberg [bibcite key=rosenberg1971effect]2. Entretanto, o modelo LF se ajusta melhor à sinais de voz de diferentes condições e se adequa melhor com fluxo glotal real, o que justifica seu uso. Veremos a seguir a estrutura do modelo de Liljencrants-Fant, seus parâmetros, as maneiras de usá-lo e suas principais propriedades.
O Modelo LF
O Modelo LF fornece um modelo do fluxo glotal definindo a forma de onda da sua derivada. Essa forma de onda é dada pela seguinte expressão:
(1) 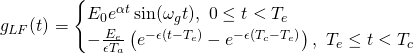
onde ![]() é o instante em que a onda que está com uma amplitude
é o instante em que a onda que está com uma amplitude ![]() deixa de ser uma onda senoidal com frequência
deixa de ser uma onda senoidal com frequência ![]() e com fator de crescimento exponencial positivo
e com fator de crescimento exponencial positivo ![]() , para ser definida por uma exponencial que vai dessa derivada de fluxo negativa até o fim do pulso em
, para ser definida por uma exponencial que vai dessa derivada de fluxo negativa até o fim do pulso em ![]() . Aqui,
. Aqui, ![]() representa o tempo efetivo de retorno do pulso, i.e., a duração de tempo que leva para uma reta, cuja inclinação é dada pela derivada da onda em
representa o tempo efetivo de retorno do pulso, i.e., a duração de tempo que leva para uma reta, cuja inclinação é dada pela derivada da onda em ![]() , sair de
, sair de ![]() e chegar em
e chegar em ![]() .3
.3
Um ciclo completo de onda da derivada do fluxo glotal e do fluxo glotal estão ilustrados na Figura 1 e na Figura 2, respectivamente, onde ![]() é o instante onde ocorre o pico da derivada,
é o instante onde ocorre o pico da derivada, ![]() é o instante onde a derivada começa a ficar negativa (onde o fluxo glotal antinge seu pico),
é o instante onde a derivada começa a ficar negativa (onde o fluxo glotal antinge seu pico), ![]() é o instante onde a derivada passa a ser descrita pela exponencial de retorno e
é o instante onde a derivada passa a ser descrita pela exponencial de retorno e ![]() o instante onde a reta com a inclinação do instante
o instante onde a reta com a inclinação do instante ![]() toca o eixo das abcissas.
toca o eixo das abcissas.


O trecho do modelo LF para o tempo de ![]() a
a ![]() é denominado de Primeira Fase. Nela ocorre a abertura do pulso glotal e é acrescentada ao sinal a influência da, assim denominada, formante glotal, com frequência
é denominado de Primeira Fase. Nela ocorre a abertura do pulso glotal e é acrescentada ao sinal a influência da, assim denominada, formante glotal, com frequência ![]() e banda passante
e banda passante ![]() . Já o trecho entre
. Já o trecho entre ![]() e o final do pulso, em
e o final do pulso, em ![]() , é denominada Fase de Retorno. Nessa fase a glote conclui seu fechamento de maneira amortecida, acrescentando ao sinal o efeito de um filto passa-baixas com frequência de corte
, é denominada Fase de Retorno. Nessa fase a glote conclui seu fechamento de maneira amortecida, acrescentando ao sinal o efeito de um filto passa-baixas com frequência de corte ![]() .4
.4
Escolha dos Parâmetros
Usualmente o modelo LF é definido com um conjunto de 5 parâmetros, mas existem várias combinações possíveis desses parâmetros. Uma possibilidade é utilizar os parâmetros da síntese direta (![]() ,
, ![]() ,
, ![]() ,
, ![]() , e
, e ![]() ). Alternativamente, pode-se utilizar
). Alternativamente, pode-se utilizar ![]() ,
, ![]() ,
, ![]() ,
,![]() e
e ![]() que são os parâmetros que aparecem naturalmente pelo processo da filtragem inversa. Esse conjunto está diretamente relacionado a um conjunto de parâmetros normalizados definidos por
que são os parâmetros que aparecem naturalmente pelo processo da filtragem inversa. Esse conjunto está diretamente relacionado a um conjunto de parâmetros normalizados definidos por ![]() ,
, ![]() ,
, ![]() ,
, ![]() e
e ![]() 5, em que:
5, em que:
(2) ![]()
![]() relaciona a frequência glotal (ou formante glotal) com a frequência fundamental (
relaciona a frequência glotal (ou formante glotal) com a frequência fundamental (![]() ),
), ![]() é o termo
é o termo ![]() normalizado por
normalizado por ![]() e
e ![]() representa o fator de inclinação definido pela proximidade entre
representa o fator de inclinação definido pela proximidade entre ![]() e
e ![]() .
.
Para uma representação mais direta dos aspectos visuais do fluxo glotal e restrições da produção vocal, outra abordagem consiste em utilizar ![]() ou
ou ![]() ou
ou ![]() no lugar do
no lugar do ![]() e para o acompanhamento direto dos aspectos no domínio da frequência, usa-se
e para o acompanhamento direto dos aspectos no domínio da frequência, usa-se ![]() em vez de
em vez de ![]() .
.
Comportamento do Modelo LF
No artigo em que o modelo LF foi proposto (Fant et al. [bibcite key=fant1985four]), bem como em Fant & Lin [bibcite key=fant1988frequency] e em Fant [bibcite key=fant1995lf] foram apresentadas propriedades do modelo LF, que definem suas características (espectrais e temporais) de acordo com os parâmetros utilizados para sua síntese.
Pra analisar o comportamento do modelo LF no tempo e na frequência, afim de verificar suas propriedades, sintetizamos o sinal do pulso glotal e do pulso glotal derivativo para diversos valores dos parâmetros definidos em 2, utilizando ![]() ,
, ![]() e freq. de amostragem
e freq. de amostragem ![]() 6. Foram tomados como base os parâmetros utilizados no Alku et al. [bibcite key=alku2019openglot] no OpenGlot para a fonação modal (
6. Foram tomados como base os parâmetros utilizados no Alku et al. [bibcite key=alku2019openglot] no OpenGlot para a fonação modal (![]() ,
, ![]() ,
, ![]() ), variando cada um dos três parâmetros, individualmente, por vez. Assim, analisamos o efeito no formato de onda e no espectro dos pulsos com a variação dos parâmetros.
), variando cada um dos três parâmetros, individualmente, por vez. Assim, analisamos o efeito no formato de onda e no espectro dos pulsos com a variação dos parâmetros.
Para ir além da visualização gráfica do pulso no tempo e no espectro, também foram sintetizados sinais de voz com os conjuntos de parâmetros utilizados na análise temporal-espectral. Optou-se por utilizar valores de formantes equivalente à vogal /a/ (![]() ,
, ![]() ,
, ![]() ).
).
Inicialmente, verificamos o efeito da variação dos valores de ![]() mantendo os demais valores constantes. Como
mantendo os demais valores constantes. Como ![]() é mantido constante, temos que a alteração de
é mantido constante, temos que a alteração de ![]() modifica os valores de
modifica os valores de ![]() (e, por consequência, de
(e, por consequência, de ![]() ). Na Figura 3 o pulso glotal e o pulso glotal derivativo no tempo com a variação de
). Na Figura 3 o pulso glotal e o pulso glotal derivativo no tempo com a variação de ![]() são ilustrados. O valor de
são ilustrados. O valor de ![]() apresenta uma forte influência no valor do pico do pulso glotal (
apresenta uma forte influência no valor do pico do pulso glotal (![]() ). O espectro do pulso derivativo é ilustrado na Figura 4. É possível observar a influência do filtro passa baixas se alterando com o aumento de
). O espectro do pulso derivativo é ilustrado na Figura 4. É possível observar a influência do filtro passa baixas se alterando com o aumento de ![]() , de forma que sua frequência de corte (
, de forma que sua frequência de corte (![]() ) se reduz.
) se reduz.

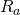 no tempo
no tempo
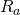 na frequência
na frequênciaSinais de voz com variação de ![]() :
:
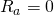 :
:
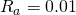 :
: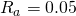 :
: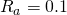 :
: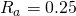 :
:
Analisamos, em seguida, os efeitos da variaçao de ![]() , fixando os demais parâmetros nos valores do modal. Como
, fixando os demais parâmetros nos valores do modal. Como ![]() é mantida constante, a alteração de
é mantida constante, a alteração de ![]() causa uma alteração diretamente proporcional em
causa uma alteração diretamente proporcional em ![]() . É possível visualizar, na Figura 5 o efeito exercido pela alteração de
. É possível visualizar, na Figura 5 o efeito exercido pela alteração de ![]() , de modo que sua variação influência o valor de
, de modo que sua variação influência o valor de ![]() e o local em que ele ocorre. A variação de
e o local em que ele ocorre. A variação de ![]() altera a formante glotal, de forma que aumentando o seu valor, há uma tendência ao reforço de dos segundo e terceiro harmônicos. Para valores mais altos de
altera a formante glotal, de forma que aumentando o seu valor, há uma tendência ao reforço de dos segundo e terceiro harmônicos. Para valores mais altos de ![]() (tipicamente,
(tipicamente, ![]() apresenta valores entre
apresenta valores entre ![]() e
e ![]() ), o segundo harmônico tende a ser mais forte do que a fundamental, como pode ser observado na Figura 6.
), o segundo harmônico tende a ser mais forte do que a fundamental, como pode ser observado na Figura 6.

 no tempo
no tempo
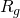 na frequência
na frequênciaSinais de voz com variação de ![]() :
:
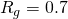 :
: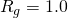 :
: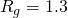 :
: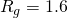 :
:
Por fim, observamos a influência da variação do ![]() , mantendo intocados em seus valores modais os demais parâmetros. Devido à constância de
, mantendo intocados em seus valores modais os demais parâmetros. Devido à constância de ![]() e de
e de ![]() , os valores de
, os valores de ![]() e
e ![]() são variados de acordo com a variação de
são variados de acordo com a variação de ![]() . Na Figura 7 podemos verificar a influência exercida por
. Na Figura 7 podemos verificar a influência exercida por ![]() no valor de
no valor de ![]() . Verificamos que o efeito de
. Verificamos que o efeito de ![]() no espectro é de difícil visualização gráfica. Entretanto, analisando a proporção entre o primeiro harmônico (frequência fundamental) e os demais harmônicos do sinal, podemos observar que o aumento de
no espectro é de difícil visualização gráfica. Entretanto, analisando a proporção entre o primeiro harmônico (frequência fundamental) e os demais harmônicos do sinal, podemos observar que o aumento de ![]() aumenta a intensidade de
aumenta a intensidade de ![]() relativamente ao restante do espectro7, como pode ser observado na Figura 8.
relativamente ao restante do espectro7, como pode ser observado na Figura 8.

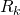 no tempo
no tempo
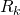 na proporção entre a frequência fundamental e seus harmônicos
na proporção entre a frequência fundamental e seus harmônicosSinais de voz com variação de ![]() :
:
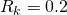 :
: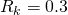 :
: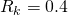 :
: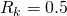 :
: :
:
Próximas Etapas
Para a continuidade do estudo da estimação de pulso glotal, nos dividiremos para estudar, implementar e relatar o desempenho de métodos presentes na literatura, que se baseiam no modelo LF. A saber, a primeira rodada de implementações vai conter os métodos propostos por Bozkurt et al. [bibcite key=bozkurt2005zeros]8, Cinnéide et al. [bibcite key=cinneide2010exploiting]9 e Dias & Ferreira [bibcite key=dias2014glottal]10.11
FANT[
ASMA]: Jurem!
[…]
HORÁCIO: Ó dia, ó noite! Isso é espantosamente estranho!
HAMLET: Portanto, como estranho, deve ser bem recebido. Há mais coisas no modelo Liljencrants-Fant, Horácio, do que sonha a tua filosofia. Mas, vamos lá; aqui, como antes, nunca, com a ajuda de Deus, […](William Shakespeare [Hamlet] sobre o Modelo LF)
[/bibshow]
Mestrando em Engenharia Elétrica e Bacharel em Engenharia Eletrônica pela Universidade Federal de Sergipe. Interessado nas áreas de Modelagem Computacional, Processamento Digital de Sinais, Processamento Digital da Fala e Reconhecimento de Padrões. Atualmente desenvolve pesquisa no estudo de modelos computacionais dos mecanismos de produção vocal.
Áreas de Pesquisa: Modelagem Computacional, Processamento Digital de Sinais, Reconhecimento de Padrões, Processamento de Sinais de Voz e Fala, Qualidade Vocal.
Estudante de Graduação em Engenharia Eletrônica na Universidade Federal de Sergipe. Áreas de interesse são Processamento Digital de Sinais, Processamento Digital da Fala e Reconhecimento de Padrões.
Estudante de Graduação em Engenharia Eletrônica na Universidade Federal de Sergipe. Interessado nas áreas de Processamento Digital de Sinais, Processamento Digital da Fala e Reconhecimento de Padrões
- Sujeito este dotado de um pequeno e comum sobrenome
- De tal maneira que duas semanas foram empregadas, pois, na árdua composição desse relatório, que só foi concluído então nos últimos momentos possíveis para o seu envio
- Ó dia, ó noite! Isso é espantosamente estranho!
- Portanto, como estranho, deve ser bem recebido
- Utilizá-los-emos para que seja realizada a análise das propriedades fornecidas pelo modelo
- Vede pois que não escrevemos Hertz. Egregiamente, expressamos da maneira adequada a frequência de amostragem. De forma alguma agimos em pusilânimidade diante de alguma possível reação belicosa por meio da professora Raíssa
- Que se enfatize, pois, que não necessariamente ocorrerá um aumento na intensidade do primeiro harmônico, porém certamente haverá uma redução na intensidade dos demais harmônicos
- João Marcus
- Vitor Magno
- Jônatas
- Vocês não devem jamais, me vendo em tais momentos, cruzar os braços assim, mexer a cabeça assim, ou pronunciar frases suspeitas, como “Ora, ora, eu já sabia”, ou “Se nós quisessemos, podíamos”, ou “Se tivéssemos vontade de, quem sabe?”, ou “Existem os que, se pudessem…”, ou ambigüidades que tais pra darem a entender que conhecem segredos meus. Não façam nada disso, e a graça e a misericórdia os assistirão quando necessitarem. Jurem.




1 thought on “Há mais coisas entre o Liljencrants e o Fant do que supõe vossa vã filosofia”