Considere que temos uma bolsa com 10 bolas, cada uma numerada com um dos números inteiros de um dígito. Ao tirarmos uma dessas bolas da bolsa teremos uma probabilidade de 1/10 de que essa bola seja o número 2. O mesmo ocorre para as demais bolas. Mas vamos fazer um experimento, se você fosse tentar adivinhar qual número de 0 a 9 eu estou pensando, quanta certeza você teria desse seu palpite?¹ Você pode dar uma porcentagem dessa certeza? Talvez você tenha notado que a probabilidade de um evento é uma medida de certeza desse evento. Faz sentido ?

Por exemplo, considere $X$ a variável que modela o evento “localização do Professor Jânio pré-aula” em duas posições $\{x_1 =$ na árvore, $x_2 =$ outro lugar $\}$ . Qual a probabilidade de $x_1$ ? Vamos dizer que seja 0.8. Consequentemente $p(x_2) = 1-p(x_1) = 0.2$ , desta forma, modelamos $X$ baseados na certeza que temos sobre as saídas deste evento.

Mas e se eu quiser uma medida de incerteza? Faz sentido dizer que a incerteza é o inverso da certeza, não é ? Então, já temos um primeiro passo a seguir. Vamos colocar matemática no meio para deixar as coisas mais certinhas. Considere o evento que modelamos anteriormente. Assim temos que:

$C = p(x_1) = 0.8 \equiv 80\%$

sendo $C$ nossa certeza de que Jânio estará na árvore. Nossa primeira estimativa de incerteza foi o inverso da certeza, ou seja:

$I = \frac{1}{C} = \frac{1}{p(x_1)} = \frac{1}{0.8} = 1.25$

sendo $I$ nossa incerteza que Jânio estará na árvore. Temos um problema agora, se tivermos absoluta certeza que ele estará lá (ele segredou a algum fofoqueiro) nossa medida de certeza deveria ser $C = 100\%$ usando a incerteza como o inverso da certeza obteríamos $I = \frac{1}{1} = 1$ , quando na verdade $I$ deveria ser 0. Podemos resolver isso aplicando o logaritmo ao nosso inverso ², assim teríamos:

$I = log(\frac{1}{C})$

que para o caso de certeza total é $I = log(1) = 0$ , e para os outros casos ainda temos que nossa incerteza decresce quando nossa certeza cresce.

Sem querer querendo, chegamos ao que Shannon chamou de informação da observação de um evento aleatório. Se quisermos saber a incerteza média do evento $X$ basta tirar a média das incertezas da seguinte forma:

$I_m(X) = C_1. I_1 + C_2.I_2$

já que as certezas (probabilidades) já são parâmetros de ponderação. Colocando na linguagem formal temos que a incerteza de uma observação do evento $X$ é dada por:

$h(x) =I(x) = log(\frac{1}{p(x)})$

E a incerteza média do evento $X$ é dada por:

$H(X) =I_m(X) = \sum_{i=1}^{N}{p(x_i)log(\frac{1}{p(x_1)})}$

sendo N o número de observações possíveis.

Chegamos novamente onde Shannon chegou, e $I_m(X)$ é a entropia da variável $X$ dada em “bits”³ se o logaritmo for de base 2, “dits” ⁴ se for de base 10 e “nats” ⁵ se for de base $e$ .

Mas o que podemos tirar da entropia de um processo?

Várias coisas, o exemplo mais citado é o de compressão de dados.

Ex:

Um curioso resolveu fazer o levantamento das linguagens de programação que os alunos do departamento de engenharia elétrica usam para processar seus dados. No total ele entrevistou 200 alunos dos cursos de elétrica e eletrônica e obteve os seguintes resultados:

Rendered by QuickLaTeX.com

O curioso gerou duas tabelas: a que vimos acima e uma outra com a resposta de cada entrevistado guardada em uma linha. Esta tabela é parecida com a que vemos abaixo.

Rendered by QuickLaTeX.com

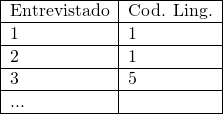
A segunda coluna corresponde ao código da linguagem selecionada. Podemos ver aqui, que cada linha terá uma segunda coluna com um byte ocupado (considerando que seja um inteiro). Vamos fazer alguns cálculos relacionados à primeira tabela:

Calculando a probabilidade de cada uma das linguagens temos:

$P(x)=\{\frac{22}{200},\frac{140}{200},\frac{4}{200}, \frac{19}{200}, \frac{15}{200}\}$

Consequentemente, suas respectivas incertezas serão:

$I(x)=log_2(\frac{1}{P(x)}) = \{3.1844 , 0.5146 , 5.6439 , 3.3959 , 3.737\}$ ;

Considere que o curioso te mandou preencher uma nova tabela imitando a tabela 2, porém agora, substituindo os números da segunda coluna por dígitos binários (curioso e cruel). São 4 linguagens de programação possíveis e o desconhecimento de programação, assim para usar quantidades de dígitos iguais para todos os elementos, temos que usar pelo 3 bits para representa-los sem repetição. Mas…. Vamos pensar como preguiçosos agora. Para adiantar nosso trabalho, podemos atribuir uma quantidade menor de dígitos para os elementos que têm menor incerteza (já que eles se repetem mais e podemos preencher a tabela mais rápido) e uma quantidade maior de dígitos para os elementos que possuem maior incerteza (já que eles aparecerão menos e não teremos tantos para preencher). Vamos usar, então, a seguinte codificação para os elementos:

Rendered by QuickLaTeX.com

Assim, colocaremos 140 – 1’s na tabela, 22 – 00’s, 19 – 010’s, 15 – 0111’s e 4 – 0110’s (pobres pessoas que ainda pegam circuitos 1 com Prof José Leite). Totalizando 317 dígitos guardados, ou 317 bits, em média, escrevemos 1,585 bits por linha. Vamos agora calcular a incerteza média desses dados:

$H(X)=I_m (X) = 3.1844 \frac{22}{200} +0.5146\frac{140}{200}+ 5.6439 \frac{4}{200} +3.3959 \frac{19}{200} + 3.737 \frac{15}{200} = 1.4263$

$H(X) = 1.4263$ bits

Coincidência? Acho que não! A entropia de um processo dá um limite inferior de bits por elemento para uma codificação com taxa de erro arbitrariamente pequeno. Essa codificação foi feita usando o algoritmo de códigos de Huffman, que é assunto para outro post.

Outra informação importante que podemos tirar da entropia é uma ideia de quantos elementos o processo possui efetivamente ⁶, a sua cardinalidade. Isso pode ser estimado a partir do seguinte cálculo:

$C(X) = k^{H(X)}$

em que $C(X)$ é a cardinalidade da fonte de dados⁷, $k$ é a base do logaritmo e $H(X)$ é a entropia do processo.

Ex:

Considere dois eventos $X = \{x_1, x_2, x_3, x_4, x_5\}}$ e $Y=\{y_1, y_2, y_3, y_4, y_5\}$ com as respectivas distribuições de probabilidade: $P(x) = \{0.2, 0.2, 0.2, 0.2, 0.2\}$ e $P(y) = \{0.005, 0.33, 0.33, 0.33, 0.005\}$ . Quando calculamos a entropia dos dois eventos⁸ temos:

$H(X) = 2.3219$ bits

$H(Y) = 1.6599$ bits

Sabemos que os eventos possuem 5 possibilidades cada, de fato $2^{H(X)} =5$ , mas por que $H(Y)$ deu menor ( $2^{1.6599} = 3.16$ )? Porque o que $C(Y)$ encontra é uma estimativa de cardinalidade efetiva, ou seja, quantos elementos possíveis realmente fazem a diferença quando colhemos muitas amostras.

Massa, tudo isso é muito bonito, mas como eu calculo a entropia de um evento que está acontecendo agora?

Tipo você vai me dizendo um monte de letra e eu tenho que estimar a entropia do que você está pensando? Sim. Bom, a resposta simples é “estimando a probabilidade dos símbolos e ir calculando a entropia enquanto você vai me dizendo as letras”. Aliás, vamos fazer esse experimento. Gere uma sequência de letras de forma aleatória e vá estimando a probabilidade de cada uma dessas letras a cada ciclo de geração. Com essa probabilidade parcial, você pode estimar a entropia do processo usando a definição de entropia.

Isso tudo serve para valores discretos, mas e se eu estiver realizando um experimento e for colhendo dados contínuos? Aí teremos que estimar a sua entropia diferencial. Definida como:

(1) $\begin{equation*}h_x = \int_S p_X(x)log(\frac{1}{p_X(x)})dx\end{equation*}$

⁹

ela não é uma medida de incerteza em si, e sim uma medida de variação de incerteza, ou, incerteza relativa. Relativa a que? Ao pedacinho $dx$ . Veja só, considere a distribuição de probabilidade apresentada na Figura 1 para um evento aleatório $X$ .

Figura 1. Uma distribuição de probabilidade.

Qual a probabilidade de uma observação de $X$ estar entre dois valores $x_1$ e $x_2$ ? É a integral da função que descreve a probabilidade entre esses dois pontos, ou seja:

$P_{12} = \int_{x_1} ^{x_2} p_X(x) dx$

que é um número que representa sua certeza, desta forma, podemos calcular a incerteza nesta região usando $I_{12} = log(\frac{1}{P_{12}})$ . Ao calcularmos a incerteza em todos os possíveis intervalos $\[x_1 , x_2)$ podemos tirar o seu valor médio usando as probabilidades como medida de ponderação, ou seja:

$\sum_{k=-\infty}^{\infty} P_{\Delta x} (k) I_{\Delta x} (k) \Delta x$

sendo $\Delta x = x_2-x_1$ .

Repare que, o valor de incerteza para a distribuição da Figura 1, será maior nas pontas e mínimo no meio. Se tivermos uma distribuição mais “aberta”, teremos mais pontos com valor afastados do 0, enquanto se tivermos uma “fechada” teremos mais pontos com valor próximo de 0. Então ao calcular a média das incertezas, faz sentido dizer que as distribuições mais largas terão média maior que as distribuições mais estreitas, já que a relação entre probabilidade e incerteza será mais constante nas largas e mais brusca nas apertadas. De fato, ao calcularmos a entropia diferencial para uma distribuição Gaussiana obtemos:

(2) $\begin{equation*}h_G = \frac{1}{2} ln(2 \pi e \sigma ^2)\end{equation*}$

vendo que a entropia depende apenas do seu parâmetro de “espalhamento”, a variância. Isso é verdade para outras distribuições também, mas vou deixar para você verificar isso.

Mas, voltando à sua pergunta, como estimar a entropia do experimento contínuo?

Bom, existem 3 formas de estimar entropia diferencial (pode ser argumentado que na verdade são apenas 2, e se pensarmos bem, podemos dizer que é apenas 1¹⁰): baseado em ajuste de distribuição de probabilidade, baseado em discretização dos espaço e baseado em contagem de vizinhos.

Baseado em ajuste de distribuição de probabilidade

Esta abordagem estima a distribuição de probabilidade da massa de dados e calcula a entropia baseada nessa distribuição usando a fórmula da definição de entropia diferencial.

Por exemplo, considere que a massa de dados que estamos estudando gerou o seguinte histograma:

É razoável dizer que a distribuição desses dados é uniforme e varia entre 0 e 1. Desta forma, podemos estimar a entropia diferencial por meio da fórmula resultante de 1 para a distribuição uniforme, que é:

$h_U=log(b-a) = log(1) = 0$

sendo $a=0$ e $b=1$ neste caso.

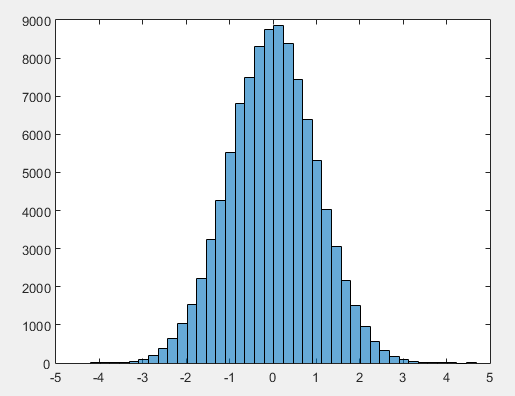
Da mesma forma, se a nossa massa de dados gerar um histograma como este:

É um galo(de cabeça)? É um morro? É a barriga do seu tio? Não! É uma gaussiana!

podemos chutar que a função que descreve a distribuição desses dados é uma gaussiana. A gaussiana tem entropia diferencial calculada a partir da equação 2, então devemos estimar o desvio padrão desses dados, que foi $\sigma$ =1.0032, assim temos:

$h_G = \frac{1}{2} ln(2\pi e \sigma^2) = 2.0517$ bits

Baseado em discretização do espaço

Considere que ao coletar dados de um experimento, obtivemos a seguinte distribuição de amostras:

Vimos que podemos calcular a incerteza de uma região a partir da probabilidade dessa região ocorrer, ou seja, podemos particionar o espaço que contém as amostras em pequenas células, e encontrar a incerteza de cada uma dessas células. Para isso, precisamos definir o tamanho da célula. Vamos considerar uma célula de lado unitário para iniciarmos, assim, teremos um conjunto de células como podemos ver na Figura 2.

Figura 2. Particionamento com célula de lado unitário

O próximo passo é contar quantos pontos estão em cada célula (criar um histograma) e atribuir o valor de contagem a essa célula. Com a contagem feita, teremos que fazer com que isso se torne uma distribuição de probabilidade. Para isso, faremos com que a integral $\int Q(x)dx =1$ , sendo $Q(x)$ a contagem de amostras no interior de um pequeno intervalo $dx$ . No nosso caso, temos uma distribuição 2D, então temos que usar $Q(A)$ como a contagem de amostras dentro de uma pequena área $dA$ , desta forma devemos normalizar o histograma para que $\int Q(A) dA =1$ . Ao fazer isso, teremos a distribuição de probabilidade representada pela Figura 3.

Figura 3. Distribuição de probabilidade dos dados.

Com o valor de probabilidade $\hat{p}_i$ em cada célula, podemos calcular sua incerteza e consequentemente sua entropia a partir da seguinte fórmula:

(3) $\begin{equation*}\hat{h}=\sum_i \hat{p}_i log(\frac{1}{\hat{p}_i}) dA\end{equation*}$

em que $dA$ é a área da célula, que no nosso caso $dA=1$ . Após esse processo, foi calculado que $\hat{h}$ =6.0872 bits para esse espaço amostral.

Caso nossos dados fossem apresentados em 3 dimensões o $dA$ se tornaria $dV$ e teríamos de contar as amostras dentro de cada célula 3D (cubo). Mais detalhes no tutorial “Meu primeiro estimador de entropia”.

Baseado em contagem de vizinhos

Uma abordagem semelhante à anterior (alguns podem até argumentar que é a mesma) porém, ao invés de segmentar o espaço em células de tamanho definido e sem sobreposição entre elas, aqui é definido um tamanho de célula centrada em uma amostra e são contadas as amostras que estiverem no interior desta célula. Diferente? Não muito, justamente por isso existe a discussão. Vamos ver uma forma de fazer isso.

Considere a distribuição dada na Figura 4. Vamos definir uma célula de lado r ao redor de um ponto qualquer. Na Figura 5 podemos ver essa célula para três tamanhos diferentes de r, 1, 0.5 e 0.25. Para estimar o quão provável um ponto é, podemos contar quantos dos pontos estão situados dentro da célula de tamanho r centrada neste ponto. Este número é então dividido pelo total de pontos, obtendo um valor de densidade referente ao ponto em que a célula está centrada.

Figura 4. Distribuição dos pontos de um experimento.

Figura 5. Exemplos de células centradas em um ponto com r iguais a 1, 0.5 e 0.25.

No nosso exemplo estamos usando um conjunto de pontos amostrados de uma distribuição normal unitária. Assim, naturalmente, os pontos que estiverem próximos à origem do plano terão uma densidade maior que os pontos mais afastados. Na Figura 6 podem ser vistos os valores de densidade para os pontos vistos nas Figuras 4 e 5 para uma célula de lado r=1.

Figura 6. Densidade dos pontos amostrados, normalizada.

Apesar de chamarmos de densidade, o que obtivemos na Figura 6 não é uma PDF, já que temos apenas pontos com valores da densidade em suas posições. Para tornarmos esses pontos em uma PDF devemos definir como a probabilidade varia com o espaço. Já temos algo parecido com isso usando nossos pontos, podemos então dizer que esse valor de densidade é constante dentro da área de influência de cada ponto. Área de influência? É a área ao redor do ponto, podemos dizer que é a área gerada pelo quadrado com lado igual ao dobro da distância até o seu vizinho mais próximo. Podemos então normalizar os valores de densidade usando a área de influência de cada ponto. Agora sim, temos uma função densidade de probabilidade.

Com a função densidade de probabilidade podemos calcular a entropia diferencial simplesmente usaremos a equação 3. Mais detalhes no tutorial “Meu segundo estimador de entropia”.

Relação entre dimensão e entropia de um processo

Como já vimos até agora, a entropia de um processo pode ser usada como uma medida de “espalhamento” dos seus dados na escala logarítmica, ou seja, podemos obter uma medida do volume (comprimento ou área, depende apenas da dimensão dos dados) que a massa de dados ocupa a partir da sua entropia por meio da seguinte equação¹¹:

(4) $\begin{equation*}V_{ef}=2^{h}\end{equation*}$

Vamos fazer um teste disso, considere um conjunto de dados amostrados a partir de duas distribuições uniformes X =[0,2] e Y=[0,1]. Ao extrair 5000 amostras teremos o gráfico visto na Figura 7. A área ocupada pelo gráfico, naturalmente, é igual a 2, então é de se esperar que ao calcularmos a entropia desta massa de dados e elevarmos ela à base do logaritmo encontremos algo em torno de 2. De fato, a entropia resultante foi 0.9864 bits, ou seja, $2^0.9864 \approx 2$ .

Considere agora o conjunto de dados formados pela mesma distribuição uniforme X mas agora com $Y = 0.5 sin(15\pi x)$ . O gráfico resultante da extração de 5000 amostras pode ser visto na Figura 8.

Podemos ver que essa distribuição tem uma estrutura de uma linha, afinal é uma senoide. Faz sentido calcular a área ocupada no espaço por uma senoide? Acho que não, já que uma linha é praticamente unidimensional. Exatamente! Quando os dados estão representados em uma estrutura que não é a que eles realmente possuem, neste caso representado em 2D quando são 1D, o cálculo de entropia não faz muito sentido e o valor resultante não pode ser usado como medida de espalhamento real. Doido né? Pois é.

Sobre o Autor

Luiz Miranda Cavalcante Neto

Possui graduação em Engenharia Elétrica com habilitação em Eletrônica pela Universidade Federal de Sergipe (2014) e mestrado em Engenharia Elétrica pela Universidade Federal de Sergipe (2017). Foi professor voluntário da Universidade Federal de Sergipe no período de 2015/1 lecionando a disciplina de Circuitos Digitais. É Professor substituto de Ensino Básico, Técnico, Tecnológico e Superior do Instituto Federal de Sergipe no Campus Lagarto (IFS-Lagarto). Tem experiência na área de Engenharia Elétrica, com ênfase em Robótica e Reconhecimento de Padrões.

Se você chutou o número 3, parabéns! Você merece uma paçoquinha
Agora você me pergunta: “Por quê não usar simplesmente o complemento ( 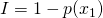$I = 1-p(x_1)$ ) ao invés do inverso?” E eu respondo: Porque isso na verdade é a probabilidade dos outros eventos ocorrerem, e não uma medida de quão incerto você está da sua previsão.
Binary Units
Decimal Units
Natural Units
Ou seja, quanto elementos irão aparecer com quantidade significativa durante os experimentos com novos dados
Quando se fala em estudo de entropia, falar da fonte de dados pode ter alguns sentidos, aqui o que me refiro é a caixa que cospe os dados que você, realizador do experimento, observa
Usando o log com base 2
Sendo 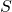$S$ o espaço constituído pela região em que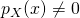 $p_X(x) \neq 0$
Estimar a PDF e calcular a entropia discreta dentro de intervalos
Se a base do logaritmo for 2

Biochaves

A entropia e alguns dos seus estimadores

Luiz Miranda Cavalcante Neto

Deixe uma resposta Cancelar resposta

Posts recentes

Categorias

Se inscreva na nossa Newsletter!