[bibshow file=ref.bib]

Objetivos

Estimar, de maneira síncrona, o pulso glotal de Rosenberg [bibcite key=rosenberg1971effect] que melhor aproxima temporalmente o pulso do sinal de voz, utilizando um banco de pulsos glotais e comparando o espectro de cada um dos pulsos com o espectro de um sinal de voz. Assim, é feito o uso de sinais de voz sintetizados, de acordo com a metodologia apresentada no relatório anterior, para a verificação dos resultados. Espera-se que o pulso glotal seja estimado perfeitamente para esses sinais sintetizados.

Metodologia

Modelo de Rosenberg para o pulso glotal

O modelo para o pulso glotal de Rosenberg [bibcite key=rosenberg1971effect] é dado pela seguinte expressão [bibcite key=Rabiner1978]:

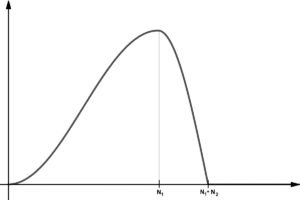
(1) $\begin{equation*} g[n]=\begin{cases} \frac{1}{2}\left(1-cos\left(\frac{\pi n}{N_1} \right) \right), & 0\leq n \leq N_1\\\\ cos\left(\frac{\pi\left(n-N_1\right)}{2 N_2} \right), & N_1\leq n \leq N_1+N_2\\ 0, & \text{para os demais casos} \end{cases} \end{equation*}$

em que $N_1$ e $N_2$ modelam o tempo de abertura e de fechamento da glote, respectivamente, como ilustrado na Figura 1. Comumente, na literatura, $N_1>N_2$ .

**Figura 1** – Pulso glotal de Rosenberg

Estimação de frequência fundamental por autocorrelação

Para a estimação de frequência fundamental ( $f_0$ ) baseada na autocorrelação do sinal, dado um sinal digitalizado $x[k]$ , a função de autocorrelação empírica $\phi[k]$ de um sinal pode ser definida como segue [bibcite key=Rabiner1978]:

(2) $\begin{equation*} \phi[k]=\sum_{m=-\infty}^{\infty} {x[m]x[m+k]} \end{equation*}$

em que se pode inferir que o valor máximo da função de autocorrelação é atingido quando $k=0$ . Também se faz notável que, para sinais periódicos, a função de autocorrelação do sinal apresenta a propriedade de manter-se periódica, com o mesmo período do sinal. Isso indica que para $k=nP$ (em que $P$ é o período e $n$ é um número inteiro qualquer), $\phi[0]=\phi[k]$ , sugerindo, assim, que a cada ciclo o valor máximo da função de autocorrelação é atingido. Assim, a estimação de $f_0$ é feita por meio dessas propriedades para encontrar o período $P$ do sinal e, consequentemente, a frequência fundamental do sinal.

Método para a estimação do pulso glotal

O processo proposto para a estimação do pulso glotal utiliza a frequência fundamental do sinal analisado, obtida por meio da autocorrelação do sinal, para gerar o banco de pulsos. Com o valor estimado da $f_0$ foi possível determinar o tamanho do pulso, em amostras, $N_G$ ( $N_G=\frac{1}{f_0}$ ). Assim o banco de pulsos foi então gerado assumindo, empiricamente, que $N_G\geq N_1+N_2$ , $round(0.3\cdot N_G)\leq N_1 \leq N_G-1$ e $round(0.1\cdot N_G)\leq N_2 \leq N_G-N_1$ .

Calculando os espectros por FFT (Fast Fourier Transform) [bibcite key=mcclellan2003signal], o espectro de cada pulso do banco é comparado ao espectro do sinal de entrada por meio do erro quadrático médio. Levando em conta a resposta espectral do pulso de Rosenberg, espera-se que o pulso que apresentar o menor erro indicará o que melhor aproxima o pulso real.

Verificação dos resultados

Para verificar a acurácia do método implementado, foram utilizados sinais sintetizados de acordo com a metodologia proposta no relatório anterior. Assim, foi feita a comparação entre o pulso estimado e o pulso utilizado para a síntese.

Resultados

A implementação do método proposto ainda não está completa, de forma que existem alguns problemas a serem resolvidos. Os resultados preliminares se mostraram inadequados, como pode ser observado na Figura 2.

**Figura 2** – Resultado atual da estimação

Conclusão e Próxima Etapa

Uma averiguação mais detalhada da implementação é necessária para que seja possível a obtenção de bons resultados com o método proposto. Assim, a próxima etapa dará continuidade a esse método, buscando solucionar os problemas encontrados. Caso os resultados com os sinais sintetizados se apresentem adequados, será feita, também, a comparação com sinais reais de voz que possuam seus respectivos sinais eletroglotográficos [bibcite key=ferrand2001speech].

[/bibshow]

Sobre o Autor

Jônatas Cruz Santos

jonatascrs@live.com | CV Lattes

Mestrando em Engenharia Elétrica e Bacharel em Engenharia Eletrônica pela Universidade Federal de Sergipe. Interessado nas áreas de Modelagem Computacional, Processamento Digital de Sinais, Processamento Digital da Fala e Reconhecimento de Padrões. Atualmente desenvolve pesquisa no estudo de modelos computacionais dos mecanismos de produção vocal.

Áreas de Pesquisa: Modelagem Computacional, Processamento Digital de Sinais, Reconhecimento de Padrões, Processamento de Sinais de Voz e Fala, Qualidade Vocal.

Sobre o Autor

João Marcus Silveira

johnnymarcus7@gmail.com | CV Lattes

Estudante de Graduação em Engenharia Eletrônica na Universidade Federal de Sergipe. Áreas de interesse são Processamento Digital de Sinais, Processamento Digital da Fala e Reconhecimento de Padrões.

Sobre o Autor

Vitor Magno Bezerra

CV Lattes

Estudante de Graduação em Engenharia Eletrônica na Universidade Federal de Sergipe. Interessado nas áreas de Processamento Digital de Sinais, Processamento Digital da Fala e Reconhecimento de Padrões

Biochaves

Estimação de Pulso Glotal utilizando Banco de Pulsos Paramétricos

Objetivos

Metodologia

Modelo de Rosenberg para o pulso glotal

Estimação de frequência fundamental por autocorrelação

Método para a estimação do pulso glotal

Verificação dos resultados

Resultados

Conclusão e Próxima Etapa

Jônatas Cruz Santos

João Marcus Silveira

Vitor Magno Bezerra

Deixe uma resposta Cancelar resposta

Posts recentes

Categorias

Se inscreva na nossa Newsletter!